4x4x4 Cube Tutorial (Beginners Method)
The 4x4x4 Cube, also known as the “Rubik’s Revenge,” is an advanced twisty puzzle that introduces additional layers, increasing complexity compared to the 3x3x3 cube. Unlike the standard 3x3x3, the 4x4x4 does not have fixed centerpieces, which adds unique challenges such as “parity errors.” However, the core solving principles remain the same, and by following this step-by-step guide, you can master solving the 4x4x4 using the beginner’s method.
Introduction
- Structure of the 4x4x4 Cube: The 4x4x4 cube consists of twenty-four center pieces, twenty-four edge pieces, and eight corner pieces. Unlike the 3x3x3 cube, there are four center pieces per face and two pieces for each edge.
- Solving Approach: We will solve the 4x4x4 in three main stages: 1) Solve the centers, 2) Pair the edge pieces, and 3) Solve like a 3x3x3 cube. This approach will also include handling parity errors, which are unique to even-layer cubes.
Step-by-Step Solution for the 4x4x4 Cube
Step 1: Understanding the Notation
The notation for the 4x4x4 cube is an extension of the 3x3x3 notation, with some added layers:
- R (Right): Rotate the entire right layer clockwise.
- r (Right Inner): Rotate the inner right layer (second layer from the right) clockwise.
- L (Left): Rotate the entire left layer clockwise.
- l (Left Inner): Rotate the inner left layer (second layer from the left) clockwise.
- U (Up): Rotate the entire upper layer clockwise.
- u (Upper Inner): Rotate the inner upper layer (second layer from the top) clockwise.
- D (Down): Rotate the entire down layer clockwise.
- d (Down Inner): Rotate the inner down layer (second layer from the bottom) clockwise.
- F (Front): Rotate the entire front layer clockwise.
- f (Front Inner): Rotate the inner front layer (second layer from the front) clockwise.
- B (Back): Rotate the entire back layer clockwise.
- b (Back Inner): Rotate the inner back layer (second layer from the back) clockwise.
- Wide Turns (w): Turn two outer layers simultaneously in the direction indicated (e.g., Rw means turning both R and r layers).
Step 2: Solving the Centers
- Solve the White Center:
- Choose any face to be the white face and start by grouping all four white center pieces together. You can achieve this by moving center pieces around without disturbing the already-placed ones.
- Basic Moves to Arrange Centers:
- Use wide moves and inner layer moves (e.g., r U r’) to position the centerpieces without disturbing solved ones.
- Solve the Opposite Yellow Center:
- Move to the opposite face and repeat the process to solve the yellow center.
- Make sure that while you align the yellow centerpieces, you do not disturb the white ones. Use wide moves like u’ Rw U Rw’ to achieve this.
- Solve the Remaining Four Centers:
- For the remaining centers (green, blue, red, and orange), you need to solve them one by one.
- Pair up two pieces at a time, align them in the correct rows, and then insert them into their correct positions by turning them around the cube using slice moves (e.g., r U r’ U’).

Step 3: Pairing the Edges
- Pair All 12 Edge Pieces:
- Pair the edges by locating two matching edge pieces and moving them next to each other using inner slice moves (u, u’, d, d’).
- Algorithm to Swap Edges: If an edge is misaligned, use: l’ U L U’ l.
- Continue this process for all twelve edges. The goal is to pair all the edges such that they align correctly like a single edge piece on a 3x3x3 cube.
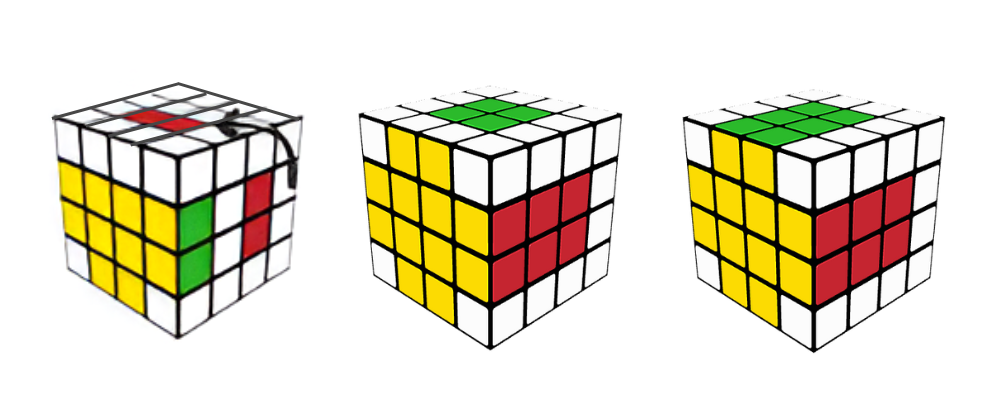
Step 4: Solve Like a 3x3x3 Cube
- Solve the First Two Layers (F2L):
- Once all edges are paired, solve the cube as a 3x3x3 using the same method: solve the cross, insert corners, and solve the second layer.
- Remember that the paired edges act like single edges from this point on, so you can use familiar algorithms.
- Orient the Last Layer (OLL):
- Perform the standard 3x3x3 OLL algorithm to orient the last layer edges and corners.
- Possible Parity Case:
- You may encounter an edge parity case where only one edge is flipped incorrectly. Use the following algorithm to fix it:
Algorithm for OLL Parity: r2 B2 U2 l U2 r’ U2 r U2 F2 r F2 l’ B2 r2
- You may encounter an edge parity case where only one edge is flipped incorrectly. Use the following algorithm to fix it:

Step 5: Permute the Last Layer (PLL)
- Permute the Last Layer:
- Use the standard 3x3x3 PLL algorithms to permute the last layer.
- Possible Parity Case:
- You may encounter a parity case where two edge pieces are swapped (a situation that does not occur on a 3x3x3). Use the following algorithm to fix it:
Algorithm for PLL Parity: Rw2 F2 U2 r U2 Rw’ U2 l U2 Rw U2 F2 Rw2
- You may encounter a parity case where two edge pieces are swapped (a situation that does not occur on a 3x3x3). Use the following algorithm to fix it:
Additional Notes and Exceptions:
- Parity Errors:
- OLL Parity: Occurs when there is a flipped edge that cannot happen on a 3x3x3. This is handled after the edges are oriented.
- PLL Parity: Occurs when two pieces are swapped incorrectly. Use the PLL parity algorithm to fix this.
- Handling Complex Moves:
- Pay close attention to the wide turns (w) and inner layer moves (r, l, etc.). These are essential for solving the 4x4x4, especially when dealing with parity cases.
- Centerpiece Orientation:
- Unlike the 3x3x3, the 4x4x4 cube does not have fixed centerpieces. This means you can freely move the centers around while pairing edges or during the early steps, which can help simplify certain moves.
Tips and Tricks:
- Practice Pairing Edges:
- Spend extra time practicing edge pairing, as this is one of the most challenging parts for beginners. Focus on learning how to pair edges efficiently using slice moves.
- Learn Key Parity Algorithms:
- Memorize the two primary parity algorithms (OLL and PLL parities) to handle these cases smoothly.
- Efficient Finger Tricks:
- Practice using finger tricks to execute algorithms faster. This will save time and improve your overall speed in solving the 4x4x4.
- Avoid Cross-Color Confusion:
- While solving centers and pairing edges, it is easy to get confused between similarly colored pieces. Make sure to double-check each piece before performing any algorithm.
Conclusion:
The 4x4x4 cube introduces new complexities, such as parity errors and additional pieces, but it follows the same logical principles as the 3x3x3. By mastering the basics of center solving, edge pairing, and handling parity errors, you can efficiently solve the 4x4x4 cube. The key is to practice each step until you are comfortable with all moves and algorithms.
