Pyraminx Cube (LBL or Layer By Layer Method)

1. Introduction

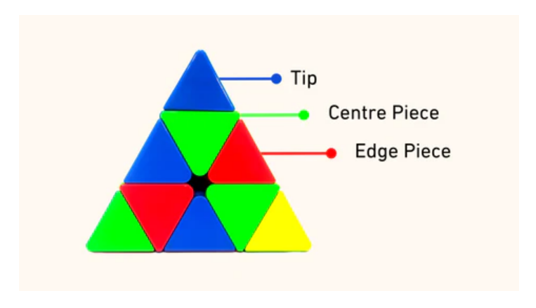
The Pyraminx is a triangular pyramid-shaped puzzle with four axial pieces, six edge pieces, and four trivial tips. Solving the Pyraminx using the Layer-by-Layer (LBL) method is relatively simple, as it involves solving one face at a time, starting with the bottom layer.

Part 1: Layer-by-Layer (LBL) Method

Step 1: Notation Overview

Before solving the Pyraminx, it is essential to understand the notations:

U: Clockwise rotation of the upper vertex.
U’: Counterclockwise rotation of the upper vertex.
L: Clockwise rotation of the left vertex.
L’: Counterclockwise rotation of the left vertex.
R: Clockwise rotation of the right vertex.
R’: Counterclockwise rotation of the right vertex.
B: Clockwise rotation of the back vertex.
B’: Counterclockwise rotation of the back vertex.

For Detailed Pyraminx Cube Learn More

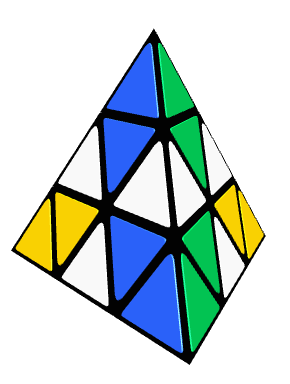
Step 2: Solve the Tips

Align the Tips: Each of the four tips of the Pyraminx can be rotated independently. Turn each tip until its colour matches the adjacent pieces on the center vertices. This step is straightforward and does not require any algorithms.

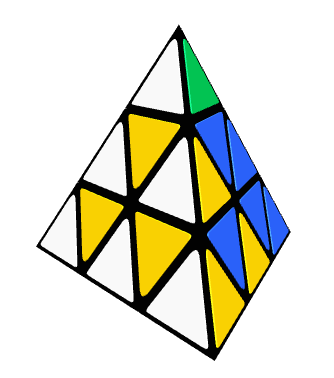
Step 3: Solve the First Layer

Choose a Base Colour: Select a colour (we will use yellow as an example) to start solving the base layer.
Position the Centrepieces: Ensure the centrepiece colours match with the tips you aligned in the previous step.
Insert the Edge Pieces: Locate the three yellow edge pieces and place them between the yellow center and the adjacent centers.

Algorithm to Insert an Edge Piece:

If the yellow edge is in the top layer:

- - Position the edge piece directly above its intended slot.
  - Use the algorithm R U’ R’ or L U L’ to place it correctly. Repeat this process for all three edge pieces.

Step 4: Solve the Second Layer

Look for Misplaced Edge Pieces in the Top Layer: Identify the edge pieces that belong to the second layer but are incorrectly placed or oriented.
Position the Edge Pieces Correctly: Perform the following algorithms to move the edge pieces to their correct positions:

Right Edge Piece Insert (when moving from top to bottom right):
Algorithm: R U R’ U’ R U’ R’
Left Edge Piece Insert (when moving from top to bottom left):
Algorithm: L’ U’ L U L’ U L

Repeat these algorithms as needed until all the edge pieces are correctly positioned in the second layer.

Step 5: Orient the Last Layer (OLL)

Check the Orientation of the Last Layer (Top Color, Green in This Case):
- The goal is to get all three remaining edge pieces oriented correctly so that the top colour matches.

Algorithm for Correcting the Orientation (Sune Algorithm):

Algorithm: R U R’ U R U2 R’
Perform this algorithm until the top layer edges are all oriented correctly.

Step 6: Permute the Last Layer (PLL)

Check the Positions of the Last Layer Edges:
The goal is to permute (swap) the edges until they are all in their correct positions.
Algorithm for Correcting Edge Permutation:

Adjacent Edge Swap (Cycle 3 Edges):
Algorithm: U R U’ L’ U R’ U’ L

Repeat this until all edges are correctly positioned.

Conclusion for Layer-by-Layer (LBL) Method:

By following these steps, you can solve the Pyraminx cube using the Layer-by-Layer method. This method is beginner-friendly and lays the foundation for more advanced methods.

Pyraminx Cube Tutorial - Advanced L4E (Last 4 Edges) Method

Step-by-Step Advanced L4E Method

Step 1: Build the First Block

Choose a Colour and Block (Two Edges and One Center) to Start:
- Select a colour (e.g., blue) to solve the first block.
- Align the first two edges with their corresponding centrepiece.
Position the Edges Correctly:
- Use simple rotations or the following basic algorithm to position the two edges adjacent to the correct centrepiece.

Basic Algorithm to Position Edges:

Algorithm: U’ L U L’ or U R’ U’ R

Repeat until the two edges are correctly aligned with the centrepiece.

Step 2: Identify the Last 4 Edges (L4E) Case

After building the first block, the next goal is to solve the remaining four edges (last layer) simultaneously. Depending on the positions of these four edges, there are several specific cases to recognize. Here are the most common and advanced cases you may encounter:

L4E Cases and Algorithms:

Case 1: 3-Cycle Edges Clockwise
- Description: Three edges are out of place and need to cycle clockwise.
- Algorithm: U’ L’ U L U’ L’ U L
Case 2: 3-Cycle Edges Counterclockwise
- Description: Three edges are out of place and need to cycle counterclockwise.
- Algorithm: U R U’ R’ U R U’ R’
Case 3: Adjacent Edge Swap
- Description: Two adjacent edges need to swap places.
- Algorithm: R’ L R L’
Case 4: Opposite Edge Swap
- Description: Two opposite edges need to swap places.
- Algorithm: L U’ L’ U L U’ L’
Case 5: Two Edges Correct, Two Edges Misoriented
- Description: Two edges are correctly positioned, but two others need orientation.
- Algorithm: U R U’ L U R’ U’ L’
Case 6: All Edges Correct but Misoriented
- Description: All four edges are in the correct positions, but their orientation is incorrect.
- Algorithm: R’ U’ R U’ R’ U R
Case 7: All Edges Correct (Skip Case)
- Description: All edges are already correctly oriented and positioned.
- No Algorithm Needed: Proceed to adjust the tips if necessary.

Step 3: Apply the Appropriate Algorithm

Once you identify which case the last four edges represent, apply the corresponding algorithm to solve them.
Repeat the algorithms if needed until all edges are oriented and positioned correctly.

Step 4: Adjust the Tips if Necessary

After solving all the edges, ensure all the tips are correctly aligned. If any tips have been accidentally moved during the previous steps, simply rotate them to match the adjacent centrepieces.

Conclusion for Advanced L4E Method:

By recognizing these specific cases and applying the correct algorithms, you can efficiently solve the Pyraminx Cube using the L4E method. This advanced method minimizes the number of steps needed and is ideal for speed cubing.